
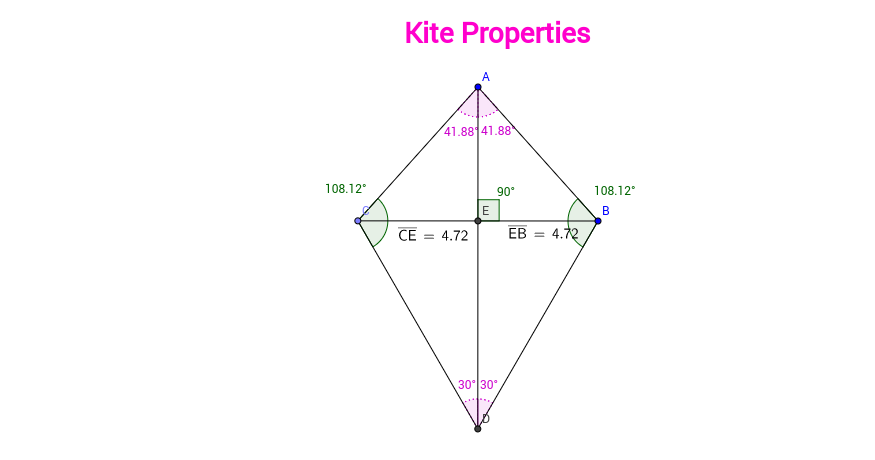
That does not matter the intersection of diagonals of a kite is always a right angle.Ī second identifying property of the diagonals of kites is that one of the diagonals bisects, or halves, the other diagonal. Sometimes one of those diagonals could be outside the shape then you have a dart. In every kite, the diagonals intersect at 90 °. The two diagonals of our kite, K T and I E, intersect at a right angle.

It is possible to have all four interior angles equal, making a kite that is also a square. Where two unequal-length sides meet in a kite, the interior angle they create will always be equal to its opposite angle. If your kite/rhombus has four equal interior angles, you also have a square. Your quadrilateral would be a kite (two pairs of adjacent, congruent sides) and a rhombus (four congruent sides). Your kite could have four congruent sides. Then you would have only a quadrilateral. The other two sides could be of unequal lengths. You could have one pair of congruent, adjacent sides but not have a kite. This makes two pairs of adjacent, congruent sides. To be a kite, a quadrilateral must have two pairs of sides that are equal to one another and touching. The kite's sides, angles, and diagonals all have identifying properties. You could have drawn them all equal, making a rhombus (or a square, if the interior angles are right angles). That also means I T and T E are not equal. You probably drew your kite so sides K I and E K are not equal. Notice that line segments (or sides) T E and E K are equal. Connect point E with point K, creating line segment E K. If you end the new line further away from ∠ I than diagonal K T, you will make a convex kite.Ĭonnect the endpoint of the perpendicular line with endpoint T. If you end the line closer to ∠ I than diagonal K T, you will get a dart. Lightly draw that perpendicular as a dashed line passing through ∠ I and the center of diagonal K T. Mark the spot on diagonal K T where the perpendicular touches that will be the middle of K T. Line it up along diagonal K T so the 90 ° mark is at ∠ I.
/GettyImages-667585769-581926633df78cc2e829a2ba.jpg)
This is the diagonal that, eventually, will probably be inside the kite. The angle those two line segments make ( ∠ I) can be any angle except 180 ° (a straight angle).ĭraw a dashed line to connect endpoints K and T. Draw a line segment (call it K I) and, from endpoint I, draw another line segment the same length as K I.
#PROPERTIES OF A KITE HOW TO#
You have a kite! How To Draw A Kite In Geometry Now carefully bring the remaining four endpoints together so an endpoint of each short piece touches an endpoint of each long piece. Touch two endpoints of the longer strands together. Touch two endpoints of the short strands together. Cut or break two spaghetti strands to be equal to each other, but shorter than the other two strands. A dart is also called a chevron or arrowhead. That means two of its sides move inward, toward the inside of the shape, and one of the four interior angles is greater than 180 °. Some kites are rhombi, darts, and squares. Sometimes a kite can be a rhombus (four congruent sides), a dart, or even a square (four congruent sides and four congruent interior angles). That toy kite is based on the geometric shape, the kite.Ī kite is a quadrilateral shape with two pairs of adjacent (touching), congruent (equal-length) sides. You probably know a kite as that wonderful toy that flies aloft on the wind, tethered to you by string.


 0 kommentar(er)
0 kommentar(er)
